Журнал Потенциал

Прежде, чем изучать новые, комплексные числа, давайте вспомним числа,
которые мы знаем.
Самые простые числа — это натуральные, они обозначаются буквой  :
:
1, 2, 3, 4, 5, 6, …
С помощью этих чисел мы считаем разные объекты.
Натуральные числа мы можем складывать и умножать.
Целые числа, обозначаемые  , расширяют множество натуральных
чисел — добавляют нуль и отрицательные числа. Наличие
отрицательных чисел позволяет нам вычитать любое число из
любого, тогда как «живя» в натуральных числах, при вычитании мы
должны были всегда следить, чтобы из большего вычиталось меньшее.
Вот примеры целых чисел:
, расширяют множество натуральных
чисел — добавляют нуль и отрицательные числа. Наличие
отрицательных чисел позволяет нам вычитать любое число из
любого, тогда как «живя» в натуральных числах, при вычитании мы
должны были всегда следить, чтобы из большего вычиталось меньшее.
Вот примеры целых чисел:

Чтобы рассматривать части целого (например, три восьмых от пирога), были придуманы
дробные числа  . Их также называют рациональными:
. Их также называют рациональными:

Кроме сложения, вычитания, умножения рациональные числа можно делить друг на друга
и снова получать рациональное число (конечно, на ноль делить при этом нельзя).
Следующее множество чисел, расширяющее множество рациональных чисел — это
действительные (вещественные) числа  .
.
Задача 1[8] Задача Архимеда
править
Докажите, что существуют иррациональные числа.

Рисунок 1. Длина диагонали единичного квадрата иррациональна
Решение.
Замечание: этот подход не является строгим в современном смысле. Нужно дать определение вещественных чисел и доказать, что среди них вообще существуют иррациональные числа. Например, в Фихтенгольце это делается с помощью Дедекиндового сечения, а уж потом доказывается, что корень из двух является примером такого числа.
Точнее эта задача звучит так: докажите, что есть отрезки, длина которых не является рациональным
числом. Рассмотрим диагональ единичного квадрата. По теореме Пифагора, квадрат её длины есть

то есть

Докажем, что это число не рационально. Пусть это не так (применяем метод доказательства от противного).
Тогда есть такие натуральные
числа  и
и  , что
, что

— несократимая дробь. Возведем равенство в квадрат и умножим на
 :
:


Отсюда следует, что  четное, то есть
четное, то есть  , где
, где  какое-то
натуральное число. Получаем:
какое-то
натуральное число. Получаем:



Из последнего уравнения следует, что  тоже четное число.
Итак, мы получили, что
тоже четное число.
Итак, мы получили, что  и
и  четные числа. Но вначале мы предположили,
что
четные числа. Но вначале мы предположили,
что  несократимая дробь. Таким образом, получили противоречие.
А значит, наше предположение, что существуют натуральные
несократимая дробь. Таким образом, получили противоречие.
А значит, наше предположение, что существуют натуральные  и
и  такие, что
такие, что

неверно.
Конец решения.
Действительные числа очень обширны, с их помощью можно описывать любое количество вещества,
любой объём жидкости, длину любого отрезка. Действительные числа можно складывать,
вычитать, умножать, делить (только на ноль делить нельзя). Кроме того, можно брать корни
из неотрицательных чисел и вычислять самые разные функции, например, синус, косинус, экспоненту и др.
Действительные числа можно представлять в виде направленной прямой с выделенной точкой  .
Точке
.
Точке  соответствует число
соответствует число  . Справа находятся положительные числа, а слева — отрицательные.
Такое представление называется «числовой осью»:
. Справа находятся положительные числа, а слева — отрицательные.
Такое представление называется «числовой осью»:

а) Может ли сумма двух иррациональных чисел быть рациональна?
Если да, то приведите пример двух иррациональных чисел, сумма которых рациональна.
б) Приведите пример двух иррациональных чисел, сумма которых иррациональна.
Докажите, что сумма действительно иррациональна.
Решение
а)  ;
;
б)  .
.
Докажите, что следующие числа не рациональны
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) ![{\displaystyle \,\!{\sqrt[{3}]{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b4ef5e4e11581dcc1d84fd8afebc02a0333776b) ; е)
; е) ![{\displaystyle \,\!{\sqrt[{3}]{2}}+{\sqrt {3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9677facd50123506b2ae4356d440d1b6e081e1bd) .
.
Решение:
а) если  рационально, то и
рационально, то и  рационально, а это не так;
рационально, а это не так;
б) так же, как и в а);
в) возведите число в квадрат, и докажите, что результат не рационален.
г) аналогично доказательству иррациональности  ;
из
;
из  следует, что и
следует, что и  и
и  делятся на
делятся на  ;
;
Кроме корней натуральных чисел и, вообще, корней различных многочленов
с целочисленными коэффициентами действительные числа содержат бесконечное множество
трансцендентных чисел.
Например, число  , равное половине длины единичной окружности, является трансцендентным числом.
Число
, равное половине длины единичной окружности, является трансцендентным числом.
Число  также является трансцендентным.
Трансцендентные числа — это числа, которые
не являются корнями никакого многочлена с целыми коэффициентами.
Доказательство того, что есть трансцендентные числа, довольно сложное
и мы углубляться в эту тему не будем.
также является трансцендентным.
Трансцендентные числа — это числа, которые
не являются корнями никакого многочлена с целыми коэффициентами.
Доказательство того, что есть трансцендентные числа, довольно сложное
и мы углубляться в эту тему не будем.
Суть в том, что действительные числа содержат все возможные длины —
какой бы кусочек веревки вы не отрезали, длина его всегда будет действительным числом.
Действительные числа представляют собой полноценный набор чисел,
которого, кажется, должно хватить для любых нужд. Но это не так.
Существует ещё одно расширение чисел — комплексные числа.
В комплексных числах можно брать корни из отрицательных чисел.
Комплексные числа хороши ещё тем,
что любой многочлен имеет среди этих чисел корень. Например, уравнения

не имеют корней в действительных числах, зато в комплексных числах имеют.
Что такое комплексные числа?
править
Знакомство с мнимой единицей 
править
Число  называется мнимой единицей. Комплексное число, квадрат которого равен отрицательной единице:
называется мнимой единицей. Комплексное число, квадрат которого равен отрицательной единице:  . Однако возможны и иные варианты: в конструкции удвоения по Кэли—Диксону или в рамках алгебры по Клиффорду
. Однако возможны и иные варианты: в конструкции удвоения по Кэли—Диксону или в рамках алгебры по Клиффорду

Рисунок 2. Комплексная плоскость. Каждая точка на плоскости соответствует
комплексному числу. Координаты  и
и  соответствуют действительной и мнимой части комплексного числа.
соответствуют действительной и мнимой части комплексного числа.
Примеры вычислений с мнимой единицей:
 ;
; ;
; ;
; .
.
Вычислите следующие выражения:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
Решение
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
Определение 1
Комплексные числа  — это пара
— это пара  действительных чисел
с заданными определенным образом операциями умножения и сложения. Комплексное число
действительных чисел
с заданными определенным образом операциями умножения и сложения. Комплексное число  записывают как
записывают как

Число  называется действительной частью числа
называется действительной частью числа  ,
а число
,
а число  — мнимой частью числа
— мнимой частью числа  .
Их обозначают
.
Их обозначают  и
и  соответственно:
соответственно:

Таким образом, комплексное число задается двумя действительными числами.
Если понимать эти числа как декартовы координаты, то
получим естественное соответствие комплексных чисел и точек на плоскости
(рис. 2).
Если в случае действительных чисел мы имели числовую прямую, то в случае комплексных чисел
получаем числовую плоскость, которая называется комплексной плоскостью.
Вычислите:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
Решение
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
Вычислите:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
Решение:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
Операции сложения и умножения комплексных чисел осуществляются так,
как если бы мнимая единица  была переменной (а комплексные числа — многочленами от этой переменной),
при этом
была переменной (а комплексные числа — многочленами от этой переменной),
при этом  .
.
Докажите, что любой многочлен от  можно свести к линейному двучлену
можно свести к линейному двучлену  .
.
Вычислите:
а)  ;
б)
;
б)  ;
в)
;
в)  .
.
Решение
а)  ;
;
б)  ;
;
в)  .
.
Найдите комплексное число  такое, что
такое, что
а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  .
.
Подсказка
Пусть

. Тогда из

следует



Найдите два комплексных числа, сумма и произведение которых равны 2.
Найдите сумму  .
.
Решение:  .
.
Подсказка:
Чему равны частичные суммы  ,
,  ,
,  ,
,  ?
?
Найдите  .
.
Решение:  .
.
Подсказка:
Чему равно  ?
?
Найдите все  , для которых верно равенство
, для которых верно равенство  .
.
Решение:
 ,
,
 ,
,
 .
.
Подсказка:
 .
.
Проверьте правильность следующих утверждений:
а) Сумма и разность чисто мнимых чисел есть чисто мнимое число.
б) Произведение двух чисто мнимых чисел равно действительному числу.
в) Квадрат чисто мнимого числа равен действительному отрицательному числу.
г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу.
Найдите число  , квадрат которого есть чисто мнимое число.
, квадрат которого есть чисто мнимое число.
Решение
 ,
,  .
.
Найдите число  , отличное от
, отличное от  и
и  , такое, что
, такое, что  .
.
Решение
 и
и  .
.
Найдите число, отличное от  , куб которого равен
, куб которого равен  .
.
Решение
 и
и  .
.
Найдите (отметьте) на комплексной плоскости все числа  ,
квадрат которых равен
,
квадрат которых равен
a) чисто мнимому числу;
б) действительному числу;
в) действительному положительному числу.
Решение:
а)  — две пересекающиеся прямые
— две пересекающиеся прямые  ,
,  ;
;
б)  или
или  — две пересекающиеся прямые
— две пересекающиеся прямые  ,
,
 ; в)
; в)  — одна прямая
— одна прямая  .
.
Cопряженные числа. Модуль. Деление
править
Определение 3
Пусть

Тогда число

называется комплексно-сопряженным или просто сопряженным к числу  .
.
Комплексное число  и комплексно-сопряженное к нему число
и комплексно-сопряженное к нему число  отличаются знаком мнимой части, действительная часть у них одинаковая:
отличаются знаком мнимой части, действительная часть у них одинаковая:

Докажите, что  .
.
Найдите, чему равны выражения
а)  ;
;
б)  ;
в)
;
в)  для
для  .
.
Решение
а)  ; б)
; б)  ; в)
; в)  .
.
Докажите тождества:
 и
и 
Докажите, что

Подсказка Используйте задачу 21 и метод математической индукции.
Пусть  — многочлен от
— многочлен от  . Докажите, что
. Докажите, что

Докажите, что числа  и
и  действительные.
действительные.
Докажите, что многочлен от  равный
равный

где  — произвольное комплексное число, имеет действительные коэффициенты
(если раскрыть скобки и привести подобные).
— произвольное комплексное число, имеет действительные коэффициенты
(если раскрыть скобки и привести подобные).
Докажите, что если комплексное число  является корнем трехчлена
является корнем трехчлена  , где
, где  и
и  — действительные числа, то
— действительные числа, то  тоже является корнем.
тоже является корнем.
Вычислите число  .
.
Решение
 .
.
Найдите целые  и
и  такие, что
такие, что
а)  ;
б)
;
б)  .
Как отличаются ответы для а) и б)?
.
Как отличаются ответы для а) и б)?
Найдите целые  и
и  такие, что
такие, что
а)  ;
б)
;
б)  .
Как отличаются ответы для а) и б)?
.
Как отличаются ответы для а) и б)?
Даны числа  и
и  .
Докажите, что
.
Докажите, что  ,
,  ,
,  целые числа при натуральном
целые числа при натуральном  .
Найдите
.
Найдите  .
.
Решение
 .
Подсказка При решении можно использовать формулу
.
Подсказка При решении можно использовать формулу

Чему равно  ?
?
Число  целое. Найдите его.
целое. Найдите его.
Решение
 .
.
Число  целое. Найдите его.
целое. Найдите его.
Решение
 .
.
Даны два действительных числа  и
и  такие, что
такие, что  и
и  — целые числа.
Докажите, что
— целые числа.
Докажите, что  будет целым числом при любом натуральном
будет целым числом при любом натуральном  .
.
Даны два комплексных числа  и
и  такие, что
такие, что  и
и  — действительные числа.
Докажите, что
— действительные числа.
Докажите, что  будет действительным числом при любом натуральном
будет действительным числом при любом натуральном  .
.
Покажите, что

Определение 4
Посмотрите на рисунок 2. Модуль числа  — это длина
отрезка
— это длина
отрезка  .
.

Модуль комплексного числа есть неотрицательное действительное число.
Модуль равен нулю тогда и только тогда, когда само число равно нулю.
Домножьте на сопряженные следующие числа
а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
;
д)  ;
;
е)  .
.
Докажите тождество  .
Подсказка Пусть
.
Подсказка Пусть  ,
,  .
Запишите равенство
.
Запишите равенство

которое соответствует равенству

Таким образом, утверждение последней задачи равносильно следующему утверждению:
Модуль произведения комплексных чисел равен произведению их модулей.
Идея домножения на сопряженное помогает нам определить операцию деления
комплексных чисел. Рассмотрим деление на примере:

Умножим и числитель и знаменатель на одно и то же число  (это число, сопряженное знаменателю). Получим:
(это число, сопряженное знаменателю). Получим:

В знаменателе стоит  — действительное число.
Разделить комплексное число на действительное не сложно: нужно просто действительную и комплексную
часть разделить на это число. Получаем:
— действительное число.
Разделить комплексное число на действительное не сложно: нужно просто действительную и комплексную
часть разделить на это число. Получаем:

Алгоритм деления на комплексное число аналогичен алгоритму избавления
от иррациональности в знаменателе. Например:

Комплексные числа можно рассматривать как множество пар  действительных чисел,
на котором специальным образом определены операция сложения, умножения и деления.
Паре
действительных чисел,
на котором специальным образом определены операция сложения, умножения и деления.
Паре  соответствует число
соответствует число  .
Операция сложения на этих парах определяется очевидным образом — надо просто
сложить соответствующие элементы пар:
.
Операция сложения на этих парах определяется очевидным образом — надо просто
сложить соответствующие элементы пар:

Найдем, как определяется умножение для этих пар:

Таким образом, мы можем дать такое определение комплексным числам:
Определение 5
Комплексные числа — это множество пар действительных чисел, на которых определены
операции сложения «  » и умножения «
» и умножения «  » по следующим правилам:
» по следующим правилам:


Покажите, что
а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
д)
;
д)  .
.
Такой подход к определению комплексных чисел требует доказательства
многих фактов, которые в предыдущей части (когда мы  рассматривали как некоторую переменную,
для которой выполнено
рассматривали как некоторую переменную,
для которой выполнено  ) были очевидны.
) были очевидны.
Пусть  ,
,  ,
,  комплексные числа. Докажите, что верны следующие свойства:
комплексные числа. Докажите, что верны следующие свойства:
 (коммутативность умножения),
(коммутативность умножения),
 (ассоциативность умножения),
(ассоциативность умножения),
 (дистрибутивность умножения относительно сложения).
(дистрибутивность умножения относительно сложения).
Вычитание определяется очевидным образом:

Определить операцию деления несколько сложнее.
Деление — это операция обратная к умножению. Следующая теорема
утверждает корректность операции деления.
Теорема 1 (О существовании деления)
Пусть даны два комплексных числа  и
и  .
Тогда уравнение
.
Тогда уравнение
[1]

относительно  имеет ровно одно решение.
имеет ровно одно решение.
Это решение обозначим как частное:

В принципе, мы уже научились делить в предыдущей части — нужно
просто числитель и знаменатель умножить на сопряженное, после
чего в знаменателе будет действительное положительное число, равное квадрату модуля знаменателя.
Это значит, что хотя бы одно решение у уравнения [1] точно есть.
Чтобы показать единственность решения, применим метод доказательства от противного.
Пусть у нас есть два решения уравнения [1]:


где  . Тогда после вычитания одного уравнения из другого получим
. Тогда после вычитания одного уравнения из другого получим

Но мы знаем, что модуль произведения равен произведению модулей.
Оба множителя,  и
и  , не равны нулю, значит их модули не равны нулю,
значит их произведение не может быть равно нулю, так как модуль произведения равен произведению модулей.
Поэтому последнее равенство не может быть верным,
и не может быть два разных решения у уравнения [1].
Есть другой подход к доказательству этой теоремы.
Пусть
, не равны нулю, значит их модули не равны нулю,
значит их произведение не может быть равно нулю, так как модуль произведения равен произведению модулей.
Поэтому последнее равенство не может быть верным,
и не может быть два разных решения у уравнения [1].
Есть другой подход к доказательству этой теоремы.
Пусть



Распишем  подробно:
подробно:


Последняя строчка соответствует системе из двух уравнений:

Когда эта система имеет решение? Умножим первое уравнение на  , а второе — на
, а второе — на  :
:


И сложим их:


Покажите, что

Как видите,  и
и  определяются вполне однозначно, если
определяются вполне однозначно, если  , то есть
когда комплексное число
, то есть
когда комплексное число  . Это и означает, что любое комплексное число
можно делить на любое другое, не равное
. Это и означает, что любое комплексное число
можно делить на любое другое, не равное  , комплексное число.
, комплексное число.
Геометрическая интерпретация
править
В этой части мы будем изучать различные геометрические свойства комплексных чисел:
преобразования комплексной плоскости, множества на комплексной плоскости,
геометрическую интерпретацию сложения и умножения.
Итак, комплексные числа образуют плоскость. Координатные оси на
этой плоскости соответствуют действительной и мнимой части
комплексного числа. Два числа — действительная часть  (
( ) и мнимая часть
) и мнимая часть  (
( ) — определяют комплексное число
на комплексной плоскости.
) — определяют комплексное число
на комплексной плоскости.
Преобразования комплексной плоскости
править
Поговорим о том, какие преобразования
плоскости соответствуют различным операциям с комплексными числами.
Какое преобразование плоскости переводит  в
в  ?
?
Решение
При этом преобразовании и действительная, и мнимая части увеличиваются в два раза.
Число  переходит в
переходит в  , число
, число  переходит в
переходит в  .
Все числа удаляются от точки
.
Все числа удаляются от точки  — они становятся в два раза дальше от неё,
но при этом остаются в том же направлении, что и до преобразования.
Комплексная плоскость как бы растягивается в два раза относительно точки
— они становятся в два раза дальше от неё,
но при этом остаются в том же направлении, что и до преобразования.
Комплексная плоскость как бы растягивается в два раза относительно точки  .
Смотрите рисунки 3 и 4.
.
Смотрите рисунки 3 и 4.
Примечание Это преобразование называется гомотетией относительно точки  с коэффициентом
с коэффициентом  .
Гомотетия с коэффициентом
.
Гомотетия с коэффициентом  будет сжимать плоскость в два раза относительно центра.
будет сжимать плоскость в два раза относительно центра.
Какое преобразование плоскости
а) переводит  в
в  ?
?
б) переводит  в
в  ?
?
в) переводит  в
в  ?
?
г) переводит  в
в  ?
?
д) переводит  в
в  ?
?
е) переводит  в
в  ?
?
ж) переводит  в
в  ?
?
Используйте рисунки 3—8.
 |  | 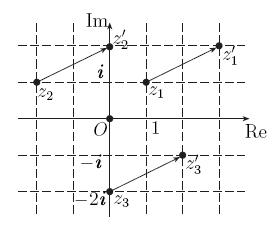 |
Рис. 3. Гомотетия растягивающая:  . . | Рис. 4. Гомотетия сжимающая:  . . | Рис. 5. Векторный перенос:  , ,  . . |
На плоскости задано две системы координат:  и
и  .
Система координат
.
Система координат  повернута относительно
повернута относительно  на 45° по часовой стрелке. Найдите, как по координатам
на 45° по часовой стрелке. Найдите, как по координатам  и
и  некоторой точки
некоторой точки  определить её координаты
определить её координаты  и
и  .
.
Подсказка
Заметьте, что если мы точку  удалим от точки пересечения
координат
удалим от точки пересечения
координат  так, что
так, что  и
и  увеличатся в два раза, то
и координаты
увеличатся в два раза, то
и координаты  и
и  увеличатся в два раза. Отсюда сразу следует, что
увеличатся в два раза. Отсюда сразу следует, что


где  ,
,  ,
,  и
и  — некоторые вещественные числа.
Осталось подобрать их. Рассмотрим точки с координатами
— некоторые вещественные числа.
Осталось подобрать их. Рассмотрим точки с координатами  равными
равными  ,
,  ,
,  ,
,  . Какие координаты
. Какие координаты  им соответствуют?
им соответствуют?
Примечание
Эту задачу можно интерпретировать по-другому:
У нас есть одна единственная система координат.
Мы осуществляем поворот всей плоскости против часовой стрелки на 45° относительно точки  , при этом оси координат
, при этом оси координат  остаются на месте.
Все точки плоскости, кроме точки
остаются на месте.
Все точки плоскости, кроме точки  переместились. Пусть точка
переместились. Пусть точка  переместилась в точку с координатами
переместилась в точку с координатами  . Найдите зависимость
. Найдите зависимость  от
от  .
.
 |  |  |
Рис. 6.  . . | Рис. 7.  . . | Рис. 8.  . . |
Какое преобразование плоскости переводит  в:
в:
а)  ;
;
б)  ;
;
в)  ?
?
Подсказка
Докажите, что модуль  (расстояние от
(расстояние от  до центра
до центра  ) при преобразованиях
не меняется. Эти преобразования — повороты. Какие именно?
) при преобразованиях
не меняется. Эти преобразования — повороты. Какие именно?
Запишите формулу  для симметрии относительно
для симметрии относительно
а) мнимой оси;
б) прямой  .
.
Запишите формулу  для симметрии относительно точки
для симметрии относительно точки  .
.
Решение
Подсказка Докажите, что искомое преобразование имеет вид  ,
где
,
где  какое-то комплексное число и учтите, что
какое-то комплексное число и учтите, что  .
.
Запишите формулу симметрии относительно прямой,
проходящей через  под углом
под углом  к действительной оси.
к действительной оси.
Решение
Обозначим  . Умножение
на это число соответствует повороту. Симметрию относительно
прямой, направленной под углом
. Умножение
на это число соответствует повороту. Симметрию относительно
прямой, направленной под углом  к действительной оси можно
представить как последовательность поворота на
к действительной оси можно
представить как последовательность поворота на  ), потом
симметрии относительно действительной оси, а потом поворота на
), потом
симметрии относительно действительной оси, а потом поворота на  :
:  .
.
Множества на комплексной плоскости и уравнения
править
Найдите (нарисуйте) множество точек (комплексных чисел)
на комплексной плоскости, для которых верно равенство

Чему равно расстояние на комплексной плоскости между числами  и
и  (запишите это число как функцию от
(запишите это число как функцию от  ,
,  ,
,  ,
,  )?
)?
Решение
 .
.
Запишите уравнение на комплексное число  ,
решением которого является круг на комплексной плоскости
с центром
,
решением которого является круг на комплексной плоскости
с центром  и радиусом
и радиусом  .
.
Где находятся комплексные числа  , для которых
, для которых
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  ?
?
Параметр  пробегает все действительные числа.
Какое множество на комплексной плоскости пробежит число
пробегает все действительные числа.
Какое множество на комплексной плоскости пробежит число  , если
, если
а)  ;
;
б)  ;
;
д)  ;
;
е)  ;
;
ж)  ;
;
з)  ;
;
и)  ;
;
к) 
Решение
Пусть  .
.
а) прямая  ;
;
б) парабола;
в) парабола — то же самое что и в предыдущем пункте, только нужно домножить
на  (повернуть на 90° и сделать сопряжение (симметрия относительно
(повернуть на 90° и сделать сопряжение (симметрия относительно  );
);
г) прямая  .
.
Подсказка Попробуйте подставить различные значения  , найти соответствующие
, найти соответствующие  и отметить их на комплексной плоскости. Затем нужно соединить их гладкой кривой.
и отметить их на комплексной плоскости. Затем нужно соединить их гладкой кривой.
Параметр  пробегает все действительные числа.
Какое множество на комплексной плоскости пробежит число
пробегает все действительные числа.
Какое множество на комплексной плоскости пробежит число  , если
, если
а)  ;
;
б)  ?
?
Решение
Пусть  .
.
а) луч, направленный вниз от точки  , так как
, так как  ;
;
б) «худая» парабола, направленная вниз.
Докажите, что треугольник с вершинами  ,
,  ,
,  подобен треугольнику
с вершинами
подобен треугольнику
с вершинами  ,
,  ,
,  .
.
Докажите, что отношение двух комплексных чисел равно действительному числу
тогда и только тогда, когда они лежат на одной прямой с  .
.
Опишите множество комплексных чисел  , для которых число
, для которых число  является
является
а) чисто мнимым;
б) действительным.
Подсказка
а) Алгебраический подход: положите  , где
, где  — любое действительное число
выразите
— любое действительное число
выразите  через
через  ; попробуйте подставить
; попробуйте подставить  ,
,  ,
,  ,
,
 ,
,  и поставить соответствующие
и поставить соответствующие  на плоскости.
на плоскости.
Геометрический подход: найдите множество чисел  на
плоскости, для которых треугольник
на
плоскости, для которых треугольник
 ,
,  ,
,  имеет прямой угол при вершине
имеет прямой угол при вершине  .
.
б) Алгебраический подход: положите  ,
где
,
где  — любое действительное число и выразите
— любое действительное число и выразите  через
через  .
.
Геометрический подход: найдите множество чисел  на
плоскости, для которых точки
на
плоскости, для которых точки  ,
,  и
и  лежат на одной прямой.
лежат на одной прямой.
Тригонометрическое представление
править
Посмотрите на рисунок 9.
Комплексное число однозначно определяется своим модулем (расстоянием до точки  )
и углом между
)
и углом между  и действительной осью — этот угол называется аргументом
комплексного числа и обозначается так:
и действительной осью — этот угол называется аргументом
комплексного числа и обозначается так:


Рис.9 Комплексное число однозначно определяется своим модулем  и аргументом
и аргументом  .
.
Определение 6
Комплексное число с модулем  и аргументом
и аргументом 
мы будем обозначать как

Докажите, что действительная и мнимая части числа  равны
равны

и


Запишите в виде  следующие комплексные числа:
следующие комплексные числа:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
Запишите в виде  (
( ,
,  ) следующие комплексные числа:
) следующие комплексные числа:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
Теорема 2
При умножении двух комплексных чисел их модули умножаются а аргументы складываются:

Доказательство теоремы отложим на потом.
Посмотрите на рисунок 10, где пояснено содержание теоремы.
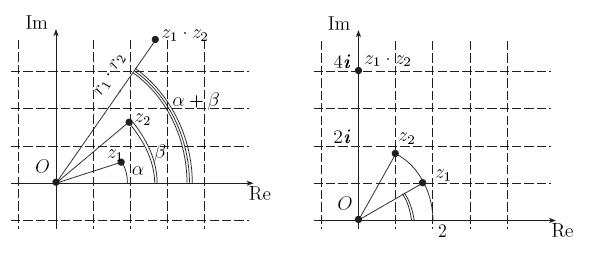
Рис. 10. При умножении чисел их модули умножаютcя, a аргументы складываются:  ,
, 
Приведем несколько примеров того, как работает эта теорема:
Пример 1.


Пример 2.

Величину  вычислим двумя способами:
вычислим двумя способами:

и в то же время

Как видите, оба метода приводят к одному и тому же результату.
Пример 3.

Величину  вычислим двумя способами:
вычислим двумя способами:

и в то же время

в итоге снова получаем  .
.
Доказательство теоремы 2.
Для доказательства теоремы достаточно показать, что

Это действительно так. Раскрывая левую часть, получим:

В скобках стоят формулы для косинуса суммы и синуса суммы.
Примечание Интересна следующая интерпретация комплексных чисел: каждое комплексное число  —
это преобразование комплексной плоскости, а именно, гомотетия относительно центра
—
это преобразование комплексной плоскости, а именно, гомотетия относительно центра  с коэффициентом
с коэффициентом  и поворот против часовой стрелки на угол
и поворот против часовой стрелки на угол  . Тогда умножение комплексных чисел соответствует
композиции соответствующих преобразований.
. Тогда умножение комплексных чисел соответствует
композиции соответствующих преобразований.
Найдите чему равно  .
.
Решение

Рассмотрите два уравнения:


Выразите из них  и
и 
Найдите значение  .
.
Покажите, что это действительное число, большее  .
.
Найдите
а)  такое, что
такое, что  ;
б)
;
б)  ;
;
в)  ;
;
Решение
а) ;
;
б)  ;
;
в)  .
.
Возвести число в  -ую степень значит возвести в
-ую степень значит возвести в  -ую степень модуль, а аргумент умножить
на
-ую степень модуль, а аргумент умножить
на  :
:

Это правило следует непосредственно из теоремы 2 предыдущего параграфа.
Задача обратная возведению в  -ую степень — это извлечение корней
-ую степень — это извлечение корней  -ой степени.
-ой степени.
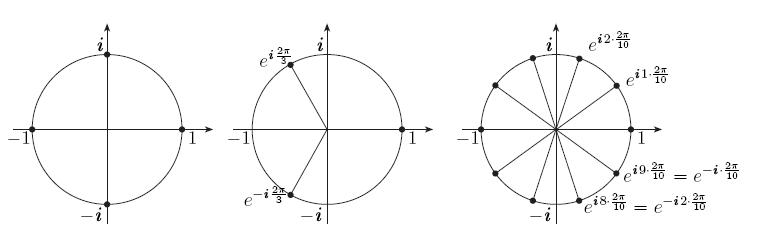
Рис. 11. Корни уравнений: а)  , б)
, б)  , в)
, в) 
Прежде, чем решать это общее уравнение, рассмотрим частный случай  ,
,  :
:

Один из корней равен  , второй равен
, второй равен  . Есть ли другие
корни? Так как
. Есть ли другие
корни? Так как  , то корни этого уравнения имеют
единичный модуль
, то корни этого уравнения имеют
единичный модуль
 и лежат на единичной окружности.
Комплексные числа, лежащие на единичной окружности, имеют вид:
и лежат на единичной окружности.
Комплексные числа, лежащие на единичной окружности, имеют вид:

После возведения в степень имеем:

Осталось найти такие  , что
, что

Последнее равенство верно, когда аргумент  кратен полному углу
кратен полному углу  :
:


Получили, что все комплексные числа вида

являются корнями уравнения  . Корень
. Корень  совпадает с корнем
совпадает с корнем  .
.
Для  эти числа отмечены на рисунке 11(в).
эти числа отмечены на рисунке 11(в).
Найдите все корни уравнения  .
.
Найдите все корни уравнения  .
.
Теперь нетрудно записать общее решение для уравнения [3].
Если  , а
, а  , то уравнение
, то уравнение

можно записать как

Числа  и
и  действительны и положительны. Модули правой и левой части должны быть равны,
Поэтому
действительны и положительны. Модули правой и левой части должны быть равны,
Поэтому

Кроме того, аргументы правой и левой части должны совпадать с точностью до  , то есть
, то есть

Из первого уравнения  определяется однозначно как
определяется однозначно как ![{\displaystyle r={\sqrt[{n}]{\rho }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d558017488f75a5a4a8d110c1100b4c928476793) .
Аргумент
.
Аргумент  может иметь
может иметь  различных значений, которые соответствуют
различных значений, которые соответствуют  ,
,  ,
,  ,
,  ,
,  .
.
Теорема 3.
Уравнение

имеет ровно  корней. Первый
корень
корней. Первый
корень  имеет модуль, равный корню
имеет модуль, равный корню  -ой степени из модуля
-ой степени из модуля
 , а аргумент — в
, а аргумент — в  раз меньший, чем аргумент
раз меньший, чем аргумент  :
:
![{\displaystyle |z_{0}|={\sqrt[{n}]{|w|}},\quad \arg z_{0}={\frac {\arg w}{n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d0323a57d950f037a2ee3f553b5bd663049ed00)
Остальные корни определяются через  :
:

Докажите эту теорему самостоятельно.
Как видите, чтобы найти все корни уравнения  , достаточно найти один корень
, достаточно найти один корень  ,
а остальные корни получатся умножением его на
,
а остальные корни получатся умножением его на  ,
,  ,
,  ,
,  .
.
Найдите все корни уравнений
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
Решите уравнения
а)  ,
,
б)  .
.
Подсказка Домножьте уравнения на  .
.
Многочлены от  — это то, что можно получить из чисел и переменной
— это то, что можно получить из чисел и переменной  с помощью умножения (в узком смысле без деления), сложения и вычитания.
Многочлены можно умножать, складывать и вычитать, получая снова многочлены.
Рассмотрим многочлены с действительными коэффициентами от переменной
с помощью умножения (в узком смысле без деления), сложения и вычитания.
Многочлены можно умножать, складывать и вычитать, получая снова многочлены.
Рассмотрим многочлены с действительными коэффициентами от переменной  .
.
Примеры многочленов:




Все многочлены, если раскрыть скобки и привести подобные слагаемые, имеют вид

Числа  называются коэффициентами многочлена.
Коэффициент
называются коэффициентами многочлена.
Коэффициент  ,
,  , называется старшим коэффициентом,
а число
, называется старшим коэффициентом,
а число  — степенью многочлена
— степенью многочлена
Найдите степени многочленов, приведенных выше.
Докажите, что при умножении многочленов их степени складываются, а
старшие (младшие) коэффициенты умножаются, то есть степень
многочлена, равного произведению двух других, равна сумме их
степеней, а старший (младший) коэффициент равен произведению их
старших (младших) коэффициентов.
Раскройте скобки и приведите подобные:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  ;
;
ж)  .
.
Умножать и складывать многочлены просто. Оказывается, их можно ещё и делить.
Рассмотрим деление многочленов на примере:

Cтепень числителя равна  , а знаменателя —
, а знаменателя —  .
Давайте вычтем и добавим к числителю
.
Давайте вычтем и добавим к числителю  , получим:
, получим:

Теперь старшая степень числителя равна  . Чтобы уничтожить слагаемое
. Чтобы уничтожить слагаемое  нужно прибавить к знаменателю
нужно прибавить к знаменателю  . Мы прибавляем и отнимаем
. Мы прибавляем и отнимаем  :
:

Дальше этот процесс продолжать нельзя, поскольку степень числителя стала меньше, чем степень
знаменателя. Таким образом, результат деления можно записать так:

Здесь  есть результат деления, а
есть результат деления, а  — остаток от деления.
— остаток от деления.
Примеры деления многочленов:





Когда остаток при делении равен нулю, то значит
первый многочлен делится на второй.
Определение 7.
Разделите один многочлен на другой с остатком:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  .
.
Решение
а) ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
д)
;
д)  ;
е)
;
е)  .
.
Известно, что  имеет корень
имеет корень  . Найдите остальные корни.
. Найдите остальные корни.
Ответ:  ,
,  .
.
Подсказка Разделите  на
на  .
.
Известно, что  имеет корень
имеет корень  . Найдите остальные корни.
. Найдите остальные корни.
Ответ:  ,
,  ,
,  .
.
Найдите все корни уравнения  .
.
Ответ:  ,
,  ,
,  ,
,  .
.
Подсказка Один из корней равен  . Проверьте это.
. Проверьте это.
Задача 76[12] Исследовательская задача
править
Пусть  .
При каких
.
При каких  и
и  многочлен
многочлен  делится
на
делится
на  ?
Например:
многочлен
?
Например:
многочлен  делится на
делится на  ,
,
 делится на
делится на  ,
многочлены
,
многочлены  ,
,  ,
,  делятся
на
делятся
на  , а
, а  ,
,  ,
,  —
не делятся на
—
не делятся на  .
.
Подсказка Заметьте, что  должно делиться нацело на
должно делиться нацело на  .
Но это не достаточное условие.
Докажите, что
.
Но это не достаточное условие.
Докажите, что  делится на
делится на  при нечетном
при нечетном  .
.
Мы умеем делить многочлены друг на друга с
остатком, и значит можно говорить о наибольшем общем делителе
двух многочленов.
Пусть  и
и  многочлены с коэффициентом 1 при старшей
степени. Тогда
многочлены с коэффициентом 1 при старшей
степени. Тогда
НОД( ,
,  )
)
есть многочлен максимальной степени с коэффициентом  при старшей степени, на
который делятся
при старшей степени, на
который делятся  и
и  .
.
Найдите
а) НОД( ,
,  );
);
б) НОД( ,
,  );
);
в) НОД( ,
,  );
);
г) НОД( ,
,  );
);
д) НОД( ,
,  );
);
е) НОД( ,
,  ).
).
Докажите, что НОД двух многочленов, есть многочлен, корни которого являются
корнями как первого, так и второго многочлена.
Найдите общие корни многочленов

Решение
НОД( ,
,  ) =
) =  ,
,  ,
,  .
.
Мы уже с вами отмечали, что некоторые многочлены не имеют действительных корней, зато имеют
комплексные корни. Например, уравнения

не имеют действительных корней, так как их правая часть положительна при любых действительных  .
Но, в то же время, комплексное число
.
Но, в то же время, комплексное число  является корнем этих уравнений.
Верна следующая теорема:
является корнем этих уравнений.
Верна следующая теорема:
Теорема 4 (Основная теорема алгебры)
Любой многочлен имеет комплексный корень.
Пояснения:
Коэффициенты многочлена могут быть как действительными, так и
комплексными.
Многочлен может иметь только действительные корни, но
это не противоречит теореме, так как действительные числа являются подмножеством
комплексных.
Степень многочлена больше либо равна  .
.
Более того, многочлен степени  обычно имеет ровно
обычно имеет ровно  корней.
А именно, верно следующее следствие из основной теоремы алгебры:
корней.
А именно, верно следующее следствие из основной теоремы алгебры:
Следствие 1
Любой многочлен степени  может быть разложен в произведение
может быть разложен в произведение  многочленов степени
многочленов степени  с комплексными коэффициентами.
с комплексными коэффициентами.
Многочлены степени  называются линейными.
называются линейными.
Например, многочлен

раскладывается в произведение линейных многочленов с действительными коэффициентами:

А многочлен

не может быть разложен в произведение действительных линейных многочленов —
для его разложения нужны комплексные числа:

Проверьте последнее равенство.
В комплексных числах любой многочлен (даже с комплексными коэффициентами)
раскладывается в произведение линейных многочленов.
Каждый множитель — линейный многочлен — дает один корень многочлена.
Почему многочлен степени  раскладывается ровно на
раскладывается ровно на  линейных множителей?
линейных множителей?
Доказательство основной теоремы алгебры довольно сложно. В конце
этой части мы рассмотрим схему одного очень популярного
интуитивного доказательства. А сейчас давайте поверим, что это
теорема действительно имеет место. Для этого вспомните задачи
1,2 и 3.
Докажите, что если комплексное число  является корнем многочлена с действительными коэффициентами,
то и сопряженное число
является корнем многочлена с действительными коэффициентами,
то и сопряженное число  также является его корнем.
Решение
Если многочлен
также является его корнем.
Решение
Если многочлен  имеет действительные максимальные коэффициенты, то
имеет действительные максимальные коэффициенты, то
 (см. задачу 23),
и если
(см. задачу 23),
и если  , то и
, то и  .
.
Найдите многочлен с действительными коэффициентами, имеющий комплексный корень  .
.
Решение:
Можно вспомнить про формулу квадратного уравнения и понять,
что второй корень будет сопряжен первому. Остается по двум корням,
 и
и  , восстановить само квадратное уравнение.
Для этого раскройте скобки
, восстановить само квадратное уравнение.
Для этого раскройте скобки  .
.
Подсказка: Среди квадратных трехчленов есть подходящий.
Найдите многочлен с действительными коэффициентами, имеющий комплексные
корни  и
и  .
Решение
.
Решение
 .
.
Используя основную теорему алгебры, докажите, что любой
многочлен с действительными коэффициентами разлагается
в произведение многочленов первой или второй степени с действительными
коэффициентами.
Решение
Можно доказывать методом математической индукции по степени
многочлена. Идея доказательства: у любого многочлена  есть
корень (основная теорема алгебры). Если это действительный корень
есть
корень (основная теорема алгебры). Если это действительный корень
 , то многочлен делится на
, то многочлен делится на  . После деления получаем
многочлен степени на
. После деления получаем
многочлен степени на  меньше — для него утверждение верно.
Если корень комплексный
меньше — для него утверждение верно.
Если корень комплексный  , то сопряженное число
, то сопряженное число
 тоже корень. А значит многочлен
тоже корень. А значит многочлен  делится на
делится на
 . После раскрытия скобок в выражении
. После раскрытия скобок в выражении
 получим квадратный трехчлен с
действительными коэффициентами. После деления получаем многочлен
получим квадратный трехчлен с
действительными коэффициентами. После деления получаем многочлен
на степени на  меньше — для него тоже утверждение верно.
меньше — для него тоже утверждение верно.
Укажите разложение на линейные множители для многочленов
а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  .
.
Решение
а) ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
;
Схема доказательства основной теоремы алгебры
править
Непрерывность — отображение кривых
править
Пусть  есть некоторый многочлен:
есть некоторый многочлен:

Тогда если мы будем медленно менять  , то число
, то число  тоже
будет меняться медленно. Если
тоже
будет меняться медленно. Если  будет двигаться по непрерывной прямой в комплексной плоскости, то
будет двигаться по непрерывной прямой в комплексной плоскости, то  тоже будет
двигаться по некоторой непрерывной кривой.
тоже будет
двигаться по некоторой непрерывной кривой.
Например, пусть  движется по окружности
движется по окружности
![{\displaystyle z=R\cdot e^{i\cdot \phi },\quad \phi \in [0,\,2\pi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a63e42930bb0f8a32786df275adb66b4f973a950)
Тогда  будет тоже двигать по некоторой
кривой в комплексной плоскости — малое изменение
будет тоже двигать по некоторой
кривой в комплексной плоскости — малое изменение  будет вызывать
малое смещение
будет вызывать
малое смещение  .
Таким образом, мы можем говорить об отображении кривых —
под действием многочлена
.
Таким образом, мы можем говорить об отображении кривых —
под действием многочлена  одна кривая превращается в другую кривую.
На рисунке 12 изображена кривая, в которую
отобразится окружность
одна кривая превращается в другую кривую.
На рисунке 12 изображена кривая, в которую
отобразится окружность  при отображении
при отображении  ,
,  .
.

Рис. 12 Образ окружности  под действием отображения
под действием отображения
 ,
, 
Доминирование старшей степени
править
Как будет двигаться  если
если  и
и  движется по окружности
движется по окружности  ?
Другими словами, как выглядит образ окружности
?
Другими словами, как выглядит образ окружности  при отображении
при отображении  ?
Заметьте, что
?
Заметьте, что  , поэтому образ этой окружности будет снова окружность,
только в то время, как
, поэтому образ этой окружности будет снова окружность,
только в то время, как  сделает один оборот по окружности
сделает один оборот по окружности  сделает
сделает  оборотов:
оборотов:


Если  сделает оборот по окружности радиуса
сделает оборот по окружности радиуса 
 ), то
), то
 сделает
сделает  оборотов по окружности радиуса
оборотов по окружности радиуса 
 ).
Свойство доминирования старшей степени заключается в том,
что при очень больших по модулю значениях
).
Свойство доминирования старшей степени заключается в том,
что при очень больших по модулю значениях  в значение многочлена
в значение многочлена
 больший вклад вносит старший член
больший вклад вносит старший член  .
.
Например, если  , то после подстановки в
, то после подстановки в  получим:
получим:


После того, как мы вынесли за скобку  , в скобках осталось только одно слагаемое,
которое не содержит
, в скобках осталось только одно слагаемое,
которое не содержит  . Все слагаемые кроме первого, при
. Все слагаемые кроме первого, при  уменьшаются и становятся
совсем маленькими и не значительными.
На рисунке 13 изображены образы трех окружностей радиусов
уменьшаются и становятся
совсем маленькими и не значительными.
На рисунке 13 изображены образы трех окружностей радиусов
 ,
,  ,
,  — чем больше радиус, тем больше его образ похож на три оборота
вокруг центра.
— чем больше радиус, тем больше его образ похож на три оборота
вокруг центра.
Непрерывность — движение кривых
править

Рис. 13 Образ окружностей  ,
,  и
и  под действием отображения
под действием отображения
 ,
,  .
.
А теперь представьте, что мы начали непрерывно менять  (например, от
(например, от  до
до  ).
Тогда образ окружности
).
Тогда образ окружности  при отображении
при отображении  ,
,  ,
постепенно будет деформироваться.
,
постепенно будет деформироваться.
- Сначала, при
 это будет просто точка
это будет просто точка  .
.
- Потом, при маленьком
 , например
, например  , вокруг точки
, вокруг точки  появится некоторая замкнутая кривая (рис. 13).
появится некоторая замкнутая кривая (рис. 13).
- Потом, при некоторых средних значениях
 , например
, например  ,будем иметь нечто необычное (рис. 12 справа).
,будем иметь нечто необычное (рис. 12 справа).
- Потом, постепенно увеличивая
 до
до  , получим три ярко выраженных оборота (рис. 13}).
, получим три ярко выраженных оборота (рис. 13}).
- При больших
 , например
, например  , обороты все больше будут сближаться друг к другу и выглядеть почти как
, обороты все больше будут сближаться друг к другу и выглядеть почти как  окружностей.
окружностей.
(рис. 13).
Во время этой деформации кривая в какой-то момент пройдёт через
точку  . Действительно, при маленьком
. Действительно, при маленьком  точка
точка  находится снаружи замкнутой кривой, а при больших
находится снаружи замкнутой кривой, а при больших  — внутри
замкнутой кривой, которая, более того, делает вокруг
— внутри
замкнутой кривой, которая, более того, делает вокруг  несколько оборотов. Это означает, что при некотором
несколько оборотов. Это означает, что при некотором  и
некотором
и
некотором  получим
получим  , и,
следовательно,
, и,
следовательно,  является корнем нашего
многочлена.
Таким образом, наш многочлен
является корнем нашего
многочлена.
Таким образом, наш многочлен  точно имеет хотя бы один комплексный корень.
Конец схемы доказательства
точно имеет хотя бы один комплексный корень.
Конец схемы доказательства
Алгебра многочленов по модулю многочлена
править
Очень часто в практике находит применение следующая конструкция.
Рассматриваются многочлены от переменной  . При этом переменная
. При этом переменная
 удовлетворяет условию, что некоторый фиксированный многочлен
от
удовлетворяет условию, что некоторый фиксированный многочлен
от  равен нулю.
Например, верно равенство
равен нулю.
Например, верно равенство

Заметьте, что из этого равенства можно заключить, что

а также, после умножения на  ,
,  , … получим
, … получим


 …
…
— то есть все степени  , начиная с
, начиная с  , могут быть выражены
через многочлены меньшей степени. А значит, любой многочлен
степени больше
, могут быть выражены
через многочлены меньшей степени. А значит, любой многочлен
степени больше  может быть упрощен до многочлена меньшей степени.
может быть упрощен до многочлена меньшей степени.
Докажите, что если  , то любой многочлен
, то любой многочлен  от
от  может быть упрощен до многочлена степени меньше
может быть упрощен до многочлена степени меньше  .
.
Подсказка Попробуйте упростить многочлен  . Покажите, что результат
совпадает с остатком при делении
. Покажите, что результат
совпадает с остатком при делении  на
на  .
.
Докажите, что если дан многочлен  степени
степени  ,
и многочлен
,
и многочлен  степени
степени  , и известно, что
, и известно, что
 , то многочлен
, то многочлен  может
быть упрощен до многочлена степени меньше
может
быть упрощен до многочлена степени меньше  и,
при этом, единственным образом.
и,
при этом, единственным образом.
Подсказка Результат упрощения равен остатку при делении  на
на  . Докажите, что
существуют единственные
. Докажите, что
существуют единственные  и
и  такие, что
такие, что

где степень  меньше степени
меньше степени  .
.
Определение 8
Найдите, чему равны следующие многочлены по модулю  .
.
Определение 9
Выражение

означает остаток при делении  на
на  .
.
Найдите, чему равно

Для многочлена  найдите многочлен
найдите многочлен  такой, что
такой, что

Для каждого ли многочлена  найдется такой
найдется такой  ?
Решение
?
Решение
 ,
,  , отсюда находим
, отсюда находим
 .
.
Докажите, что алгебра многочленов по модулю  совпадает с комплексными числами.
В каком смысле они совпадают?
совпадает с комплексными числами.
В каком смысле они совпадают?
Рассмотрите алгебру многочленов по модулю  .
Верно ли что, для каждого многочлена
.
Верно ли что, для каждого многочлена  , который не делится
на
, который не делится
на  , найдется
, найдется  такой, что
такой, что

Рассмотрите алгебру многочленов по модулю  .
Верно ли что, для каждого многочлена
.
Верно ли что, для каждого многочлена  , который не делится
на
, который не делится
на  , найдется
, найдется  такой, что
такой, что

Определение 10
Многочлен называется неприводимым, если он не может быть разложен в произведение
многочленов степени больше  .
.
а) Докажите, что в алгебре многочленов над комплексными числами не существует неприводимых многочленов степени
больше  .
б) Докажите, что в алгебре многочленов над действительными числами не существует неприводимых многочленов степени
больше
.
б) Докажите, что в алгебре многочленов над действительными числами не существует неприводимых многочленов степени
больше  — неприводимы только те квадратные трехчлены, дискриминант которых отрицателен.
— неприводимы только те квадратные трехчлены, дискриминант которых отрицателен.
Многочлены с действительными коэффициентами
по модулю любого неприводимого многочлена  изоморфны комплексным числам.
изоморфны комплексным числам.
Примечание
Изоморфность означает одинаковость с точностью до переобозначения.
Два множества элементов  и
и  с операциями сложения и умножения
изоморфны если между их элементами существует взаимооднозначное соответствие,
которое сохраняет операции сложения и умножения.
Например, пусть элементу
с операциями сложения и умножения
изоморфны если между их элементами существует взаимооднозначное соответствие,
которое сохраняет операции сложения и умножения.
Например, пусть элементу  из
из  соответствует элемент
соответствует элемент  из
из 
 — это функция, осуществляющая соответствие элементов
— это функция, осуществляющая соответствие элементов  элементам
элементам  ).
Пусть
).
Пусть  и
и  произвольные элементы
произвольные элементы  . Тогда
. Тогда

Заметьте, что операции сложения и умножения слева от знака «равно» — это операции на множестве  ,
а операции сложения и умножения справа — операции на множестве
,
а операции сложения и умножения справа — операции на множестве  .
.
Подсказка Это соответствие строится следующим образом. Любой неприводимый
квадратный трехчлен можно линейной заменой переменной  превратить в
превратить в  . По многочлену
. По многочлену  можно
найти многочлен
можно
найти многочлен  — его два коэффициента
соответствуют мнимой и действительной части соответствующего
— его два коэффициента
соответствуют мнимой и действительной части соответствующего  комплексного числа.
Действительные и комплексные числа называются числовыми полями.
Есть ещё другие числовые поля.
Если в каком-то числовом поле нет неприводимых многочленов степени больше
комплексного числа.
Действительные и комплексные числа называются числовыми полями.
Есть ещё другие числовые поля.
Если в каком-то числовом поле нет неприводимых многочленов степени больше  , то
оно называется алгебраически замкнутым.
Комплексные числа — единственное алгебраически замкнутое числовое поле,
где бесконечное (точнее несчетное) число элементов.
, то
оно называется алгебраически замкнутым.
Комплексные числа — единственное алгебраически замкнутое числовое поле,
где бесконечное (точнее несчетное) число элементов.
Матрицы — это ещё одно обобщение чисел. Мы с вами изучим матрицы  .
.
Определение 11
Примечание
Первый индекс соответствует номеру строчки, второй — номеру столбца.
Правила сложения и умножения можно коротко обозначить так:


Если бы мы рассматривали матрицы  , то правило умножения выглядело бы так:
, то правило умножения выглядело бы так:

Чтобы получить элемент матрицы  , стоящий в
, стоящий в  -ой строчке и
-ой строчке и  -ом
столбце, нужно взять
-ом
столбце, нужно взять  -ую строчку матрицы
-ую строчку матрицы  и
и  -ый столбец
-ый столбец  , а затем взять их произведение —
перемножить соответствующие элементы и сложить.
, а затем взять их произведение —
перемножить соответствующие элементы и сложить.
Пусть

Вычислите:
а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
д)
;
д)  ;
е)
;
е)  .
.
Определение 12.
Матрица

называется
единичной матрицей.
Докажите, что

для любой матрицы  .
.
Таким образом, единичная матрица обладает такими же свойствами,
как и число  — умножение на
— умножение на  не меняет число.
не меняет число.
Определение 13
Введем обозначение:

Докажите, что

то есть произведение матрицы  на саму себя дает единичную матрицу с минусом.
на саму себя дает единичную матрицу с минусом.
Определение 14
Матрицы можно умножать на число, при этом каждый элемент матрицы умножается на это число.
Например:

Покажите, что
а)  ;
б)
;
б)  ;
в)
;
в)  .
.
Раскройте скобки

Введем обозначение

Найдите результат умножения матриц  .
.
Подсказка Обратите внимание на то, что получится снова матрица вида
 , то есть матрица, у которой на диагонали (верхний левый
угол — нижний правый) стоят одинаковые числа, а два числа на
другой диагонали противоположны.
, то есть матрица, у которой на диагонали (верхний левый
угол — нижний правый) стоят одинаковые числа, а два числа на
другой диагонали противоположны.
Найдите результат умножения матриц  .
.
Покажите, что матрицы вида  с операциями сложения и умножения матриц
соответствуют комплексным числам с операциями сложения и умножения комплексных чисел.
с операциями сложения и умножения матриц
соответствуют комплексным числам с операциями сложения и умножения комплексных чисел.
На основе предыдущей задачи предположите, чему равно

Решение
 .
.
Подсказка Чему равно  ?
?
Определение 15
Найдите матрицу, обратную к матрице  , то есть найдите
, то есть найдите

Система линейных уравнений

может быть записана как

Покажите, что решение этой системы может быть записано как

- «Теорема Абеля в задачах», В. Б. Алексеев, — М.:МЦНМО, 2001.






































![{\displaystyle \,\!{\sqrt[{3}]{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b4ef5e4e11581dcc1d84fd8afebc02a0333776b)
![{\displaystyle \,\!{\sqrt[{3}]{2}}+{\sqrt {3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9677facd50123506b2ae4356d440d1b6e081e1bd)




































































































































































































































































































































































































![{\displaystyle r={\sqrt[{n}]{\rho }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d558017488f75a5a4a8d110c1100b4c928476793)




![{\displaystyle |z_{0}|={\sqrt[{n}]{|w|}},\quad \arg z_{0}={\frac {\arg w}{n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d0323a57d950f037a2ee3f553b5bd663049ed00)


































































































































![{\displaystyle z=R\cdot e^{i\cdot \phi },\quad \phi \in [0,\,2\pi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a63e42930bb0f8a32786df275adb66b4f973a950)




















































































































